Go语言的八大排序算法及其实现
·在Go语言中,可以实现多种经典的排序算法。下面我们将详细介绍八种常见的排序算法,展示它们的Go实现,并给出每种算法的时间复杂度和稳定性分析。
1. 冒泡排序 (Bubble Sort)
冒泡排序是一种简单的交换排序算法。它通过多次遍历数组,逐渐将较大的元素移动到数组的末尾。
算法描述:
比较相邻的两个元素,如果顺序错误就交换它们。
每轮遍历后,最大元素会逐渐移到数组的末尾。
重复以上步骤直到数组完全有序。
Go实现:
func bubbleSort(arr []int) []int {
n := len(arr)
for i := 0; i < n; i++ {
for j := 0; j < n-i-1; j++ {
if arr[j] > arr[j+1] {
arr[j], arr[j+1] = arr[j+1], arr[j]
}
}
}
return arr
}时间复杂度:最坏和平均时间复杂度为 O(n2)O(n2) 稳定性:稳定
2. 选择排序 (Selection Sort)
选择排序每次从未排序部分选出最小元素,将其放到已排序部分的末尾。
算法描述:
找到未排序部分的最小元素,与未排序部分的第一个元素交换。
重复以上步骤,直到所有元素有序。
Go实现:
func selectionSort(arr []int) []int {
n := len(arr)
for i := 0; i < n; i++ {
minIdx := i
for j := i + 1; j < n; j++ {
if arr[j] < arr[minIdx] {
minIdx = j
}
}
arr[i], arr[minIdx] = arr[minIdx], arr[i]
}
return arr
}时间复杂度:最坏和平均时间复杂度为 O(n2)O(n2) 稳定性:不稳定
3. 插入排序 (Insertion Sort)
插入排序通过不断将未排序的元素插入到已排序部分来构建有序序列。
算法描述:
从第二个元素开始,每次将当前元素插入到前面已排序的部分中。
对每个元素,向前遍历直到找到合适的位置插入。
Go实现:
func insertionSort(arr []int) []int {
for i := 1; i < len(arr); i++ {
key := arr[i]
j := i - 1
for j >= 0 && arr[j] > key {
arr[j+1] = arr[j]
j--
}
arr[j+1] = key
}
return arr
}时间复杂度:最坏和平均时间复杂度为 O(n2)O(n2) 稳定性:稳定
4. 希尔排序 (Shell Sort)
希尔排序是插入排序的改进,通过将数组划分为若干子序列进行排序来加快排序速度。
算法描述:
通过逐步缩小步长,将数组分割成若干组。
对每组进行插入排序,步长逐渐减少,最后当步长为1时完成排序。
Go实现:
func shellSort(arr []int) []int {
n := len(arr)
for gap := n / 2; gap > 0; gap /= 2 {
for i := gap; i < n; i++ {
temp := arr[i]
j := i
for j >= gap && arr[j-gap] > temp {
arr[j] = arr[j-gap]
j -= gap
}
arr[j] = temp
}
}
return arr
}时间复杂度:最坏时间复杂度为 O(n2)O(n2),平均时间复杂度为 O(nlogn)O(nlogn) 稳定性:不稳定
5. 归并排序 (Merge Sort)
归并排序是一种经典的分治算法,适合处理大规模数据。
算法描述:
将数组分成两部分,分别递归进行归并排序。
合并两个有序数组为一个有序数组。
Go实现:
func mergeSort(arr []int) []int {
if len(arr) > 1 {
mid := len(arr) / 2
left := mergeSort(arr[:mid])
right := mergeSort(arr[mid:])
return merge(left, right)
}
return arr
}
func merge(left, right []int) []int {
result := []int{}
i, j := 0, 0
for i < len(left) && j < len(right) {
if left[i] < right[j] {
result = append(result, left[i])
i++
} else {
result = append(result, right[j])
j++
}
}
result = append(result, left[i:]...)
result = append(result, right[j:]...)
return result
}时间复杂度:最坏和平均时间复杂度为 O(nlogn)O(nlogn) 稳定性:稳定
6. 快速排序 (Quick Sort)
快速排序是另一种分治排序算法,通常是实际应用中最快的排序算法之一。
算法描述:
选择一个基准元素,数组分为小于和大于基准的两部分。
递归对左右两部分分别排序。
Go实现:
func quickSort(arr []int) []int {
if len(arr) <= 1 {
return arr
}
pivot := arr[len(arr)/2]
left := []int{}
right := []int{}
equal := []int{}
for _, v := range arr {
if v < pivot {
left = append(left, v)
} else if v > pivot {
right = append(right, v)
} else {
equal = append(equal, v)
}
}
return append(append(quickSort(left), equal...), quickSort(right)...)
}时间复杂度:最坏时间复杂度为 O(n2)O(n2),平均时间复杂度为 O(nlogn)O(nlogn) 稳定性:不稳定
7. 堆排序 (Heap Sort)
堆排序利用堆这种数据结构来实现排序,时间复杂度为 O(nlogn)O(nlogn)。
算法描述:
构建最大堆。
交换堆顶元素和末尾元素,调整堆,重复直到数组有序。
Go实现:
func heapSort(arr []int) []int {
n := len(arr)
for i := n/2 - 1; i >= 0; i-- {
heapify(arr, n, i)
}
for i := n - 1; i > 0; i-- {
arr[0], arr[i] = arr[i], arr[0]
heapify(arr, i, 0)
}
return arr
}
func heapify(arr []int, n, i int) {
largest := i
left := 2*i + 1
right := 2*i + 2
if left < n && arr[left] > arr[largest] {
largest = left
}
if right < n && arr[right] > arr[largest] {
largest = right
}
if largest != i {
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
}
}时间复杂度:最坏和平均时间复杂度为 O(nlogn)O(nlogn) 稳定性:不稳定
8. 计数排序 (Counting Sort)
计数排序适用于范围较小的整数排序,通过计数每个元素出现的次数进行排序。
算法描述:
找到最大和最小元素。
统计每个元素的出现次数。
根据计数数组生成排序后的结果。
Go实现:
func countingSort(arr []int) []int {
max, min := arr[0], arr[0]
for _, v := range arr {
if v > max {
max = v
}
if v < min {
min = v
}
}
count := make([]int, max-min+1)
output := make([]int, len(arr))
for _, v := range arr {
count[v-min]++
}
for i := 1; i < len(count); i++ {
count[i] += count[i-1]
}
for i := len(arr) - 1; i >= 0; i-- {
output[count[arr[i]-min]-1] = arr[i]
count[arr[i]-min]--
}
return output
}时间复杂度:最坏和平均时间复杂度为 O(n+k)O(n+k),其中 kk 是计数数组的范围 稳定性:稳定
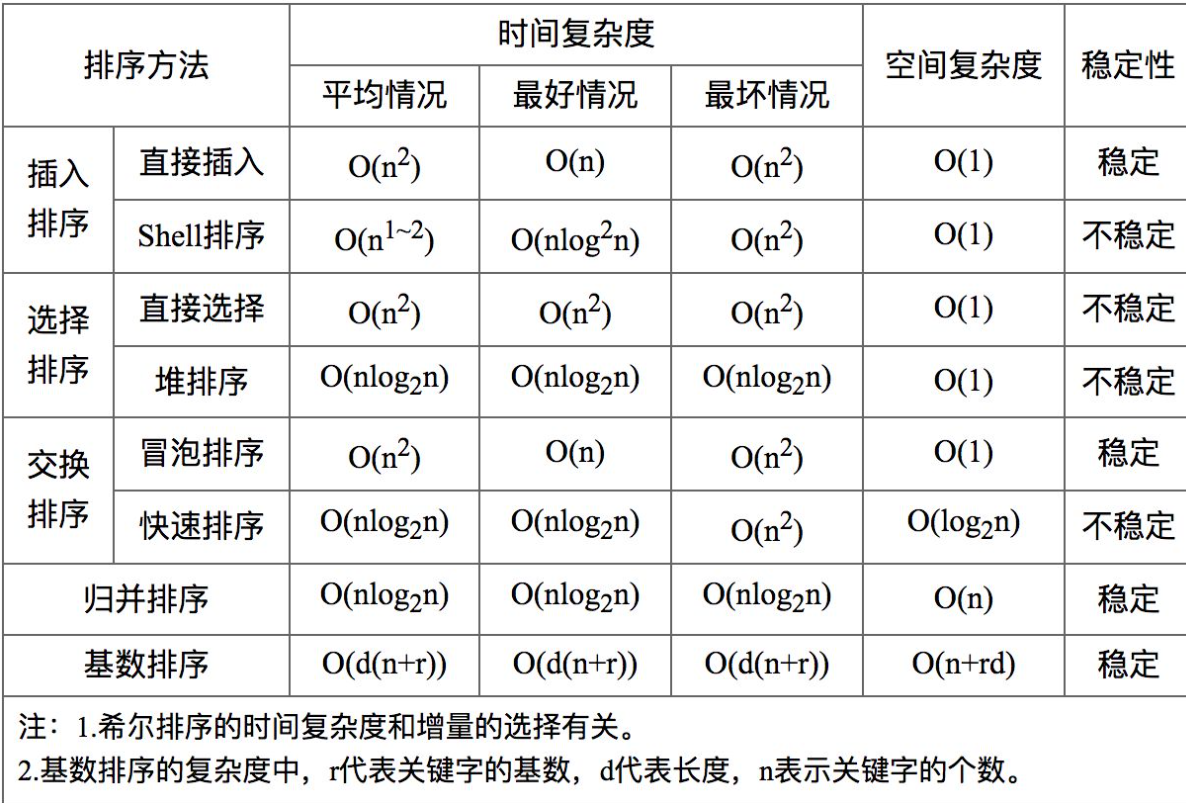
排序算法时间复杂度和稳定性总结