八大排序算法详解及Python实现
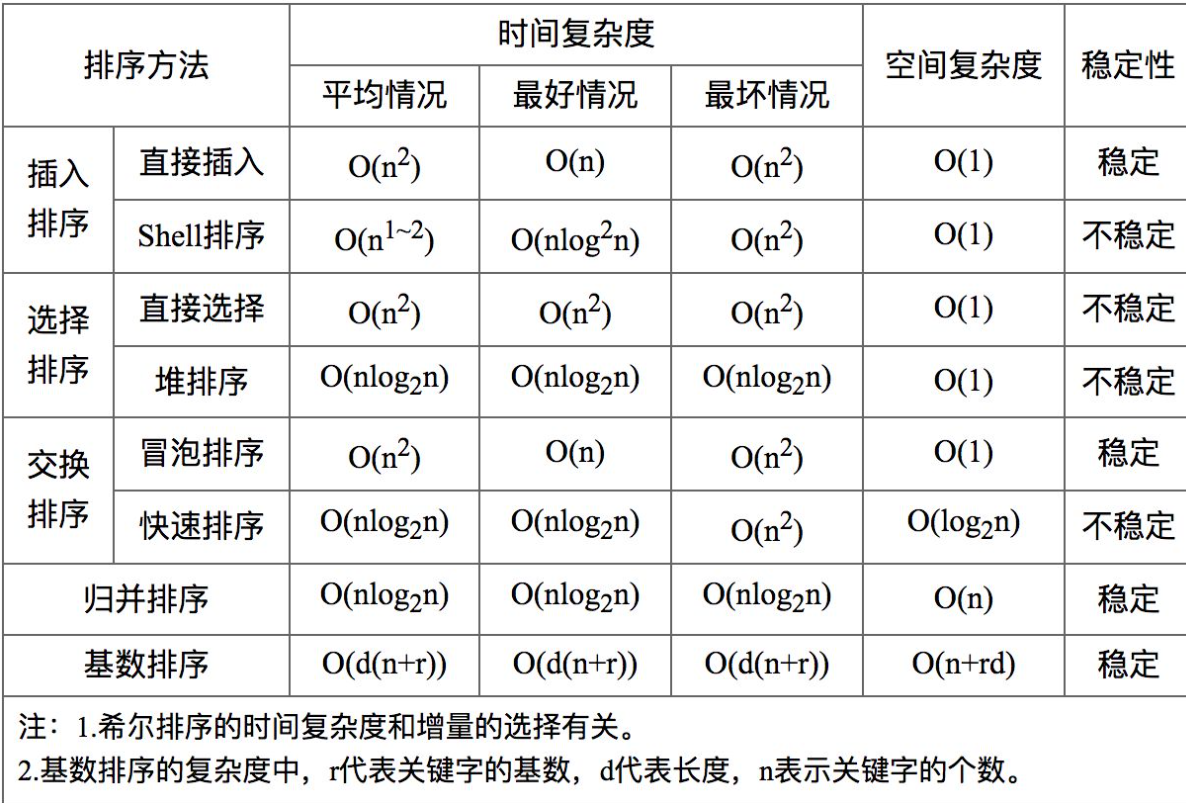
这里对八大排序算法进行了详细解释,并提供了Python实现。最后给出了各排序算法的时间复杂度及稳定性总结表。
1. 冒泡排序 (Bubble Sort)
冒泡排序是一种简单的排序算法,通过重复比较相邻的元素并交换位置,将较大的元素逐渐移动到数组末尾。
算法描述:
比较相邻的元素,如果前一个比后一个大,则交换它们的位置。
对每一对相邻元素进行同样的操作,从头到尾,这样每一轮处理后,最大的元素会被移到末尾。
忽略已排序的最后一个元素,重复上述过程,直到整个数组有序。
Python实现:
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr
2. 选择排序 (Selection Sort)
选择排序每次从未排序的部分选出最小(或最大)的元素,放在已排序部分的末尾。
算法描述:
在未排序的数组中找到最小的元素,放到数组的起始位置。
从剩下的未排序元素中继续找到最小元素,放到已排序数组的末尾。
重复上述过程,直到所有元素排序完毕。
Python实现:
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_idx = i
for j in range(i + 1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
return arr
3. 插入排序 (Insertion Sort)
插入排序通过构建有序序列,对于未排序数据,从已排序序列中从后向前扫描,找到相应位置并插入。
算法描述:
从第一个元素开始,认为它已经排序。
取出下一个元素,在已排序的元素序列中从后向前扫描。
如果该元素(已排序)大于新元素,将该元素移到下一位置。
重复步骤3,直到找到已排序的元素小于或等于新元素的位置。
将新元素插入到该位置。
重复步骤2~5。
Python实现:
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
return arr
4. 希尔排序 (Shell Sort)
希尔排序是插入排序的改进,通过将整个数组分割成若干子序列分别进行插入排序,从而加快排序速度。
算法描述:
将数组按步长gap进行分组。
对每组使用插入排序。
减小gap,重复步骤1~2,直到gap=1。
Python实现:
def shell_sort(arr):
n = len(arr)
gap = n // 2
while gap > 0:
for i in range(gap, n):
temp = arr[i]
j = i
while j >= gap and arr[j - gap] > temp:
arr[j] = arr[j - gap]
j -= gap
arr[j] = temp
gap //= 2
return arr
5. 归并排序 (Merge Sort)
归并排序是一种采用分治法的排序算法,将数组分成两个子数组,分别排序后合并。
算法描述:
分割:将数组从中间分成两部分。
递归地对两部分分别进行归并排序。
合并:将两个有序数组合并成一个有序数组。
Python实现:
def merge_sort(arr):
if len(arr) > 1:
mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]
merge_sort(left_half)
merge_sort(right_half)
i = j = k = 0
while i < len(left_half) and j < len(right_half):
if left_half[i] < right_half[j]:
arr[k] = left_half[i]
i += 1
else:
arr[k] = right_half[j]
j += 1
k += 1
while i < len(left_half):
arr[k] = left_half[i]
i += 1
k += 1
while j < len(right_half):
arr[k] = right_half[j]
j += 1
k += 1
return arr
6. 快速排序 (Quick Sort)
快速排序使用分治法,通过一个基准元素将数组分成两部分,递归地对两部分排序。
算法描述:
选择一个基准元素。
分区:将数组中小于基准元素的放在左边,大于基准元素的放在右边。
对左右两部分分别递归进行快速排序。
Python实现:
def quick_sort(arr):
if len(arr) <= 1:
return arr
else:
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quick_sort(left) + middle + quick_sort(right)
7. 堆排序 (Heap Sort)
堆排序利用堆这种数据结构来排序,时间复杂度为O(n log n)。
算法描述:
构建最大堆。
交换堆顶元素和末尾元素,将堆的尺寸减1。
调整堆以满足最大堆性质。
重复步骤2~3,直到堆的尺寸为1。
Python实现:
def heap_sort(arr):
def heapify(arr, n, i):
largest = i
left = 2 * i + 1
right = 2 * i + 2
if left < n and arr[i] < arr[left]:
largest = left
if right < n and arr[largest] < arr[right]:
largest = right
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
n = len(arr)
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
for i in range(n - 1, 0, -1):
arr[i], arr[0] = arr[0], arr[i]
heapify(arr, i, 0)
return arr
8. 计数排序 (Counting Sort)
计数排序是一种适用于整数数组的排序算法,通过计数数组记录每个元素出现的次数。
算法描述:
找出数组中的最大值和最小值。
创建计数数组,并统计每个元素出现的次数。
根据计数数组还原排序后的数组。
Python实现:
def counting_sort(arr):
max_val = max(arr)
min_val = min(arr)
range_of_elements = max_val - min_val + 1
count = [0] * range_of_elements
output = [0] * len(arr)
for i in range(len(arr)):
count[arr[i] - min_val] += 1
for i in range(1, len(count)):
count[i] += count[i - 1]
for i in range(len(arr) - 1, -1, -1):
output[count[arr[i] - min_val] - 1] = arr[i]
count[arr[i] - min_val] -= 1
for i in range(len(arr)):
arr[i] = output[i]
return arr
排序算法时间复杂度和稳定性总结